¡Empiezo nuevo curso de esos de 90 días! Esta vez sobre finanzas; ya que durante estos últimos meses me estoy dando cuenta de la importancia de entender cómo funciona el dinero, y en general la economía. Así que ahí vamos con Finance for Everyone: Smart Tools for Decision-Making, de la mano del doctor en finanzas Gautam Kaul.
Antes que nada quiero hacer una pequeña reseña hacia el docente encargado de impartir este curso, Gautam Kaul, ya que me parece fascinante el entusiasmo con el que explica todos y cada uno de los conceptos, y la cercanía que es capaz de transmitir a pesar de estar grabado en diferido. De verdad que me ha sorprendido su brillo en los ojos, y la calidez de su discurso a pesar de estar hablando a una cámara hehe.
Finanzas para todos: Los conceptos más básicos del curso
Aunque el entusiasmo del profesor por explicar todo el mundo de las finanzas en innegable, sí que hay algo de lo me gustaría hacer una breve puntualización, y esto es: su afán por usar Excel para revolver casi el 100% de los problemas.
Por un lado entiendo que cualquier persona que se dedique a día de hoy a las finanzas lo hará con Excel o con una herramienta similar, que te agiliza el trabajo de forma inhumana. Sin embargo, no me parece la mejor alternativa para un curso de completos principiantes.
A mí al menos, al principio me gusta afianzar conceptos entendiéndolos desde la base (conociendo su fórmula, de dónde se saca cada dato, etc…), y todos estos cálculos él los hace de manera demasiado automática utilizando Excel, sin proporcionarte ningún dato matemático.
Al principio cuando estás viendo los vídeos parece que entiendes todo a la perfección, y que son conceptos muy sencillos, pero más adelante cuando te toca enfrentarte a los ejercicios propuestos, te das cuenta de que en realidad solo sabes un puñado de «comandos» en Excel, y ni siquiera tienes criterio suficiente para saber en qué orden aplicarlos o dónde escribir cada dato del enunciado.
Encontrar o deducir luego cada una de esas fórmulas matemáticas correspondientes a los «comandos» de Excel no ha sido nada sencillo, y quiero aprovechar este post para dejar todas ellas apuntadas por aquí, en caso de que las necesite (yo o cualquier otra persona) en un futuro.
Breve explicación y fórmula de cada concepto en Finanzas Básicas
Por otro lado, también me di un buen golpe de realidad al ver que las finanzas no tienen tanto que ver con las matemáticas como yo creía. Mientras que las matemáticas, de alguna forma, sirven para interpretar y dar forma a datos númericos, las finanzas sirven para interpretar y dar forma a escenarios humanos, a través de datos numéricos; y esto hace una gran diferencia.
Leyenda Esencial para este post de Finanzas:
Puesto que las fórmulas que se muestran a continuación fueron poco a poco anotadas y deducidas por mí a lo largo del curso, desconozco qué letras se usan de forma estandarizada para referirse a cada concepto, así que dejo aquí un mini-guía sobre lo que significa cada letra en las siguientes fórmulas:
i – interés
Es el porcentaje que pagas o adquieres durante cada periodo. Es imprescindible tener en cuenta que por norma general el interés se presenta de forma anual (también llamado APR) mientras que los pagos o ingresos suelen tener una frecuencia mensual.
De este modo, cada vez que aparezca la letra i, será refiriéndome al INTERÉS POR PERIODO (es decir, APR/12 en caso de que los pagos sean mensuales) y expresado siempre sobre 1.
Si te dicen que el interés es de un 6%, seguramente se refieran al APR, el interés por mes será entonces de 6/12 = 0.5% y nuestra variable i valdrá 0.005, puesto que se expresa sobre 1. Esto es fundamental aunque ahora no lo parezca.
Su fórmula es la siguiente: (justo debajo veremos qué son FV y PV)
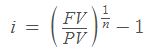
n – periodos
Con la letra n hago referencia al número de periodos estipulados.
En caso de que los pagos sean mensuales durante un total de tres años, n = 12 * 3 = 36.
Valor Actual (PV)
Utilidad 1: Conocer la aportación inicial para llegar a una cifra final
El primer concepto que se aprende en este curso, y uno de los términos más básicos que se emplean. Es el valor que tiene un depósito actual.
Para calcular el valor actual de un depósito conociendo únicamente datos del futuro (su valor en el futuro, tasa de interés y periodos transcurridos) se utiliza la siguiente fórmula:
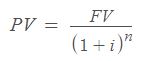
Ej: Necesitas saber cuánto dinero dejar en el banco durante 5 años al 6% de interés para que tu suma de ahorros ascienta a 20000€.
En este caso (n = 60), y (i = 0.5% = 0.005), así que neesitarás un capital incial de 14827.44€.
Como puedes apreciar, calcular el PV sirve para saber el dinero inicial que necesitarás si quieres alcanzar una cantidad específica de dinero pasados n años con un interés i.
Utilidad 2: Calcular la deuda pendiente cuando pagas siempre la misma cantidad por periodo
También se puede utilizar PV para calcular la deuda pendiente en mitad de un proceso de pagos, conociendo de antemano el pago por periodo y los periodos restantes. Este proceso tiene mucho sentido, ya que estás calculando la suma de dinero a la que asciende una aportación periódica PMT con un interés i durante n periodos.
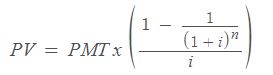
Por ejemplo: tienes que pagar $400 cada mes, durante los próximos 15 meses, pues entonces sabes que tu PV será igual al número exacto que consiga dejar el FV a cero teniendo en cuenta los pagos de cada plazo y el interés que irá disminuyendo conforme quede menos dinero en la cuenta.
Valor Futuro (FV)
Es el valor que tendrá un depósito que crece (o decrece) con un interés constante durante un periodo de tiempo determiando.
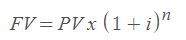
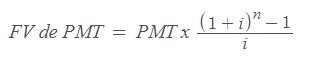
¿Qué es el interés (APR)?
El interés anual es el porcentaje acordado que se paga o se ingresa cada año.
En muchos casos los pagos se realizan mensualmente y el interés es acumulativo (es decir: ingresas un porcentaje de tu dinero actual, y esta pequeña suma extra que ingresas luego afectará al siguiente pago con interés, por lo que recibirás un poco más que la vez pasada, etc…). A esto se le llama interés compuesto.
A la hora de calcular pagos por periodos (o amortizaciones) es entonces muy importante tener en cuenta que este interés compuesto se descontará de esta manera tras cada pago.
Al final un interés anual se pacta con la claúsula de que se aplica siempre al monto total de dinero acumulado. Por este motivo cuanta mayor parte de tu deuda has pagado, menor será el interés que tengas que pagar en la próxima. Por contra partida, cuantos más periodos de pago realices, mayor será el interés acumulado que se pague al final.
Ten en cuenta que en una amortización normal siempre estás pagando un porcentaje de lo que te queda pendiente, así que es mejor pagar mucho en pocos plazos, que pagar poco en muchos plazos.
Ejemplo:
Imagina que tienes una deuda de $1000 y necesitas devolverla con un interés del 2% anual.
Antes que nada ten en cuenta que NO existe una cantidad fija a devolver si no se conoce de antemano el número de plazos que vas a usar para ello.
Podrías pensar que simplemente tendrás que devolver $1000 + un 20% de 1000. En total $1020. Pero esto no es así.
Esto solo significa que trascurrido un año habrás tenido que abonar el 2% de lo que te quede pendiente de deuda. De esta forma si a final de año decides pagar $220 ($200 de la deuda real + $20 porque es el 2% de %1000), te seguirá quedando una deuda real de $800. Por lo que si al próximo año pagas otros $200, tendrás que abonar $16 extra porque son el 2% de lo que te faltaba por pagar. Y esta operación puede extenderse hasta el infinito si cuantos más pagos hagas.
Siguiendo con este ejemplo sencillo, si cada años pagas $200 de la deuda real y tardas un total de 5 plazos en saldar tu deuda, habrás pagado intereses en valor de $60 ($20 + $16 + $12 +$8 + $4), que son exactamente el 2% de lo que cada año te faltaba por pagar.
En el mundo real esto no ocurre así, y los pagos se suelen realizar por meses. De esta manera cada mes sueles pagar un doceavo del interés pactado anualmente, ya que el interés pactado se repartirá igualmente entre cada uno de los doce meses. Siempre pagarás el mismo porcentaje cada mes, independientemente de lo que te falte por pagar.
De este modo, es más mucho peligroso tener una deuda que se extienda demasiado años, que una deuda con un alto interés anual si se paga en pocos plazos.
Interés Efectivo Anual / Effective Annual Rate (EAR / TAE)
Este interés EAR (o TAE en español) refleja mucho mejor el coste real del interés que tendrá pedir un préstamo.
Suele proporcionarlo la persona que estipula el porcentaje de interés y en él ya van incluídos algos gastos extra de gestión, mantenimiento, etc…
Interés Real (RI) a pagar en la amortización de un préstamo
Es el interés real que terminas pagando durante un número determinado de plazos a lo largo de un año.
Ya que el interés inicial se acuerda de manera anual, pero suele pagarse de manera mensual es casi imposible que este porcentaje que te da el banco (o alcualquier otro intermediaria) sea el auténtico interés que vas a terminar pagando. Este interés auténtico será casi siempre muy superior al acordado anualmente.
Su fórmula (nada fácil de intuir) es la siguiente:
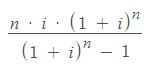
Pago por Período (PMT)
PMT sirve para saber por adelantado la cantidad fija de dinero que se pagará en cada periodo, conociendo de antemano el número de tiempo que transcurrirá y el porcentaje de interés.
Es importante ser conscientes de que el interés suele venir en porcentaje anual, mientras que los pagos se realizan mensualmente. Por este motivo en la mayoría de casos conviene usar el número de periodos como n (total de meses), y el interés como i / 12 (interés anual dividido entre doce).
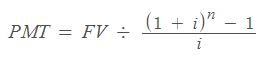
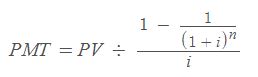
¿Cuánto cuesta un pago de varios periodos anuales con una inflación r?
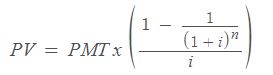
Calcular valor invertido a un interés i frente a un inflación r
Otro cálculo recurrente en finanzas es saber cuánto valdrán tus ahorros invertidos a un interés i frente a un inflación r; sin embargo no existe una fórmula directa para hacer esto.
Es tan simple como calcular cada uno por separado y sumarlos. Hasta donde yo he podido investigar NO hay una fórmula per se ya que no existe una simplificación matemática que te permita sumar varias bases iguales con diferente exponente.
Tendrás que ir calculando cada periodo el aumento de capital por interés, y luego quitarle la pérdida por inflación.
En el ejemplo de abajo (sacado del curso de finanzas) queremos calcular el valor de nuestros $11314.08 invertidos con un interés del 2.5% frente a una inflación del 5%.
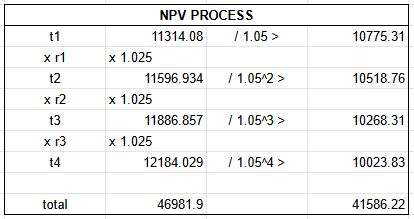
Otra forma mucho más rápida de hacer esto es utilizando excel.
Amortización
Dentro de los pagos por periodos (PMT), existe una amortización de la deuda, en la que a pesar de pagar todos los meses lo mismo, no pagas por igual deuda e interés, sino que al principio pagas poca deuda y mucho interés, y al final terminas pagando mucha deuda y poco interés.
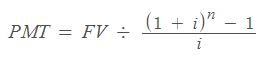
La idea es que a través de aumentar con el tiempo el pago por deuda y reducir el pago de intereses el pago por período termine siendo siempre el mismo. De ahí que pueda calcularse a través de esta fórmula.
Sin embargo, no hay que equivocarse: aunque el pago mensual sea siempre el mismo, esta forma progesiva de pagar deuda e interés hace que siempre termine saliendo más caro de lo que debería.
¿Por qué no pagas todo a partes iguales cada mes? D:
Quizás esto se debe a que cuando hacer una re-negociación del interés, ésta se aplica sobre lo que te queda de pagar de deuda real. Como al principio pagas más por los intereses que por la deuda, siempre se hará la re-negociación sobre un valor más alto que si pagaras todos los meses la misma cantidad por interés que por deuda. De esta forma el prestamista es el que sale ganando en todos los escenarios.

Deja una respuesta