Alice in Borderland es uno de los mangas que más he disfrutado estos últimos años, es parte de mi Top 10 Animes y Mangas Recomendados, y aunque plasma muy bien la psicología de todos los personajes y te obliga a empatizar con ellos y sufrir en cada juego, precisamente lo que más me enganchó a seguir leyendo fue la originalidad de cada prueba, destacando especialmente el juego del Rey de Diamantes, que me pareció notablemente interesante.
Este artículo contiene spoilers extraídos del manga oficial de Alice in Borderland. La serie en Netflix todavía no ha llegado hasta este punto, y estarás saltándote mucha información. Si de verdad estás interesado en conocer el desenlace puedes leer el manga oficial, o empezar a leer el manga donde termina la serie de Netflix.

Juego del Rey de Diamantes – Alice in Borderland
En este juego únicamente pueden participar cinco personas (cuatro personas más el rey de diamantes), y tan solo una de ellas será la que salga con vida y con la carta del Rey de Diamantes, heredando su cargo si así lo desea.
El juego «Concurso de Belleza» propuesto por el propio Rey de Diamantes se inspira en un juego descrito por el economista Colin F. Camerer en su libro Behavioral Game Theory, quien a su vez se inspiró en el experimento descrito por John Maynard Keynes con este mismo nombre. A raíz de este juego, más tarde surgió el experimento «2/3 de la Media», propuesto por Alain Ledoux. En el Concurso de Belleza original se explica un modelo de juego en el que los participantes tienen que votar a la chica más guapa según diferentes rasgos faciales, y gana el participante que más se acerque al promedio de todos los rasgos faciales votados. De este modo, para ganar no necesitas votar lo que a ti te parece más atractivo, sino lo que crees que parece más atractivo para el resto.
Concurso de Belleza – Reglas:
- Todos los jugadores seleccionan un número entre 0 y 100 en el tiempo determinado.
- La media de los valores se multiplicará por 4/5 (0,8).
- La persona que elija un número más cercano al calculado gana.
Cuando termina cada ronda:
- Todos los perdedores perderán un punto.
- Una vez que un jugador llega a -10 puntos, será bañado en ácido ardiendo.
- El último jugador que quede, sobrevivirá.
- Se introduce una nueva regla por cada jugador eliminado.
Al principio puede parecer una prueba en la que lo más influyente es la suerte que tenga cada jugador, ya que tu resultado no depende únicamente de ti, sino que se verá influenciado también por los otros cuatro jugadores. El Rey de Diamantes también estaba apostando su vida a que ganaría, así que si fuera un juego de suerte, tendría solo un 20% de posibilidades de haber mantenido su título a lo largo de la historia.
Una de las participantes también mencionó que si bien no se trata de un juego enteramente de suerte, sí que está más cerca de ser una prueba de Corazones. Sin embargo, nada más lejos de la realidad, este juego no consiste en analizar la psicología de los demás. Ya que todas las normas del juego están basadas en las matemáticas ganará aquel que sea más preciso midiendo la racionalidad de sus rivales.
Los participantes




Análisis del Juego
Ronda 1 del Concurso de Belleza
Al principio, Daimon Hinako piensa que todos sus compañeros elegirán el número 50, puesto que todos son increíblemente inteligentes y esta es la opción más segura. De este modo la media sería también 50, y multiplicado por un factor de 0,8, como indican las reglas del juego, el resultado final sería 40. Si ella desde el principio elije el número 40 la media de los cinco números será 48, que multiplicado por 0,8 terminaría dando como resultado 38.4, y ella ganaría. ¿Sencillo, no? (Espero que sí, porque esta es la parte superficial del juego).

Para sorpresa de Daimon Hinako, ella fue la que más lejos se quedó de acertar. Todos sus compañeros dedujeron que todos iban a bajar hasta elegir el número 40, y que el resultado final sería de 32, la cuestión es: si algún otro jugador elije como respuesta el 32, puede ser interesante incluso elegir el 28, 29 ó 30, bajando un pelín más la media para favorecerte sobre el resto. De esta manera el Rey de Diamantes elige el número 29 y pasa a ser el único jugador que no recibe penalización ese turno.
Si lo piensas bien, siguiendo el razonamiento anterior esta vez es posible que todos piensen que los demás jugadores elegirán el número 32, y de este modo la respuesta final pasará a ser 32 x 0,8 = 25,6. Pero si también piensan eso todos elegirán el 26, y la respuesta final sería 20,8. Siguiendo este razonamiento lógico es muy arriesgado elegir algo que no sea el 0. Sin duda, la respuesta final favorece a aquellos que redondean hacia abajo, puesto que todo será multiplicado por 0.8.
Otra forma de llegar a esta conclusión es la siguiente:
Si no se pueden elegir números por encima del 100, el resultado jamás podrá estar por encima de 80, y de este modo elegir un numero superior a 80 no tiene sentido. Si todos saben que elegir algo superior a 80 no tiene sentido, 80 se convertiría en el tope, pero entonces ningún resultado sería nunca superior a 64, por lo que elegir un numero superior a 64 no tendría sentido, etc… hasta llegar a la conclusión de que elegir un número que no sea el 0 no tendría ningún sentido.
Ronda 2 del Concurso de Belleza
Aquí ocurre algo muy interesante, y es que, como todos son jugadores altamente inteligentes no tardan nada en comprender que si todos eligen 0 como respuesta nadie ganará jamás. De este modo todos deciden apostar por ir bajando de poco en poco hacia el 0. De hecho, bajar de golpe hasta el 0 puede ser una jugada arriesgada, ya que si no habéis llegado todos a la misma conclusión, y por ejemplo los números elegidos son 0, 0, 0, 1 y 21, el que ha elegido el 1 terminará ganando.
Aquí es cuando empieza el verdadero juego: tienes que analizar la primera ronda de cada uno de tus oponentes y medir su nivel de racionalidad.
Benzo el matemático, y Keiichi el Rey de Diamantes jugaron una ronda muy inteligente. Por otro lado el estudiante de medicina jugó una ronda completamente racional mientras que el analista y la prestamista hicieron buenos cálculos pero también se dejaron llevar por el instinto.
¿Qué número elegirías para la segunda ronda?
Esta vez todos piensan similar: 32 ha sido el número entorno al que se ha jugado la primera ronda, así que el resultado final al elegir 32 ahora sería 26. Todos pensarán eso mismo, y buscarán un número entorno a 20. La pregunta es… ¿qué tan acertados estarán el resto de jugadores y qué tanto intentarán bajar la media?
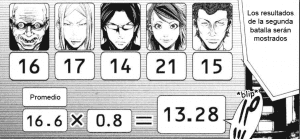
De nuevo vemos cómo la prestamista se deja influenciar brevemente por su instinto, mientras que los demás jugadores han tenido una ronda bastante acertada. Sin embargo, el Rey de Diamantes vuelve a ser el que mejor ha entendido la forma de jugar de los demás.
Ronda 3 del Concurso de Belleza
En la tercera ronda pasa algo similar: la chica no es buena eligiendo resultados matemáticamente exactos, y suele redondear, por otro lado el matemático suele elegir los resultados más racionales, sin tener demasiado en cuenta a sus competidores, mientras que el médico y el analista están comenzando a leer bien todas las jugadas excepto las del Rey de Diamantes.
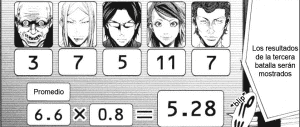
Tras la tercera ronda, Keiichi, abogado internacional y actual Rey de Diamantes es el único que no ha perdido puntos.
Ronda 4 del Concurso de Belleza
En la cuarta ronda tan solo el abogado y el médico juegan bien sus cartas: se han dado cuenta de que la prestamista sigue un proceso de pensamiento diferente al resto, y que el matemático tiene cálculos muy preciosos pero no ha logrado entender la forma de pensar de la prestamista.
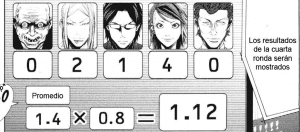
Aún así el Rey de Diamantes vuelve a dar la apuesta más precisa, y sigue sin perder puntos.
Ronda 5 del Concurso de Belleza
¿Qué elegirías tú para la quinta ronda?
Es una ronda un poco confusa, porque han ido bajando peldaños hasta llegar a este punto, en el que todos deberían de jugar entorno al 0. De hecho hubo dos jugadores que se adelantaron y ya eligieron el 0 en la ronda anterior. En este punto alcanzan el Equilibrio de Nash, un concepto de la teoría de juegos que hace referencia a los casos en los que ningún jugador puede obtener beneficios al cambiar su estrategia. Esto lo habían previsto todos en la segunda ronda: ahora si alguien elige un número diferente a 0 tiene altas probabilidades de perder.
Las apuestas de cada uno para esta ronda fueron:

Todos podrían estar eligiendo el 0 hasta que se vieran obligados a arriesgarse en alguna ronda para terminar el juego en algún momento y no morir de hambre.
El médico enseguida se percata de esto y no tarda ni una sola ronda en destrozar el Equilibrio de Nash. Además esta ronda gana la chica, quien ha seguido lanzando apuestas arriesgadas incluso en este momento.
Creo que el Rey de Diamantes iba a apostar por el número 1 en la siguiente ronda, una vez todos se hubieran dado cuenta de que votar por el 0 no servía para nada.
Ronda 6 del Concurso de Belleza
Ahora la pregunta es… ¿cómo sigue el juego?
Como has podido deducir, en la siguiente ronda todo se vuelve un poco más caótico: la chica dedice conscientemente perder esta ronda con tal de dejar en claro que elegir 0 ya no era una opción. Por otro lado el matemático apuesta a que ninguno iba a arriesgar de nuevo sus puntos, el analista entiende que todos iban a elegir un número por encima de cero, y de nuevo el médico y el abogado son los únicos que le siguen el ritmo a la chica, previendo que iba a dedicar este turno a crear más caos. Aún así, en esta ronda el médico se alza con la victoria.
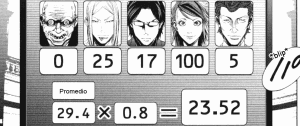
Ronda 7 del Concurso de Belleza
La siguiente ronda es el médico el que vuelve a elegir el número 100, y es la chica quien gana de nuevo. Mientras tanto el matemático sigue apostando por el 0, pensando que todos iban a valorar su vida esta vez, por encima de cualquier otra cosa.
Ronda 8 del Concurso de Belleza
Ya en la octava ronda el matemático decide cambiar de estrategia, y apostar por el 36, entendiendo que los resultados finales estaban siendo altos y ya nadie apostaba por el Equilibrio de Nash.
Para su sorpresa, ningún jugador elige perder a propósito esta ronda, así que los resultados se estabilizan un poco y tanto el médico como el abogado salen victoriosos de esta apuesta.
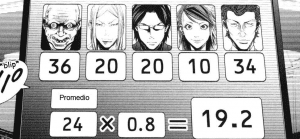
Pasada esta octava ronda en la que se produce el empate entre Keiichi y Shuntarou, el resto del juego ya no se basa en buscar una respuesta orientada a que todos los jugadores van a elegir el mismo número como referencia; para esta novena ronda todos se conocen lo suficiente como para intentar buscar con precisión la elección de cada uno de sus oponentes.
Rondas 9 y 10 del Concurso de Belleza
Para el final de la décima ronda el matemático y el analista pierden la vida, sin haber ganado ni una sola ronda.
Para el final del juego se añaden varias reglas más. La más interesante es que si varios jugadores eligen el mismo número, todos esos jugadores pierden. De esta forma consigues evitar posibles escenarios en los que todos apuesten por el 0, o por el 1…
No quiero seguir analizándolo mucho más porque la dinámica del juego ya está vista, y en las rondas que quedan se dan deducciones psicológicas muy interesantes, pero no tan relacionadas con el juego en sí.
Las posibilidades para que jueguen las tres personas que quedaban son las siguentes:
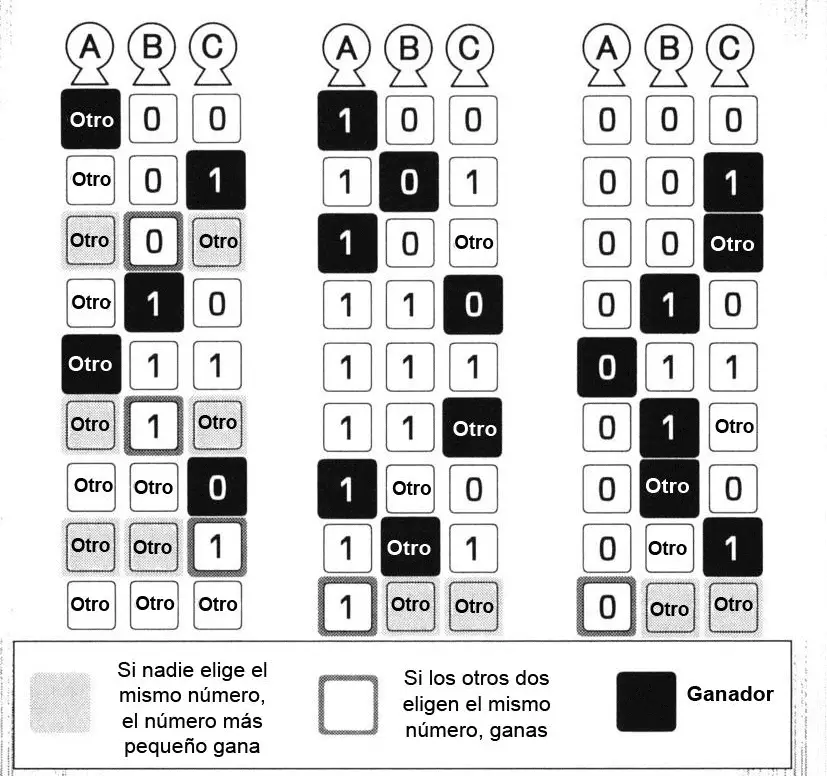
Estrategia para Jugar
Sería muy curioso tener la oportunidad de jugar a este juego con tus amigos, o por internet, como quien juega una partida de póker… pero ¿qué estrategias serían las más óptimas para ganar en este juego de Diamantes?
Puede seguir pareciendo que contra rivales desconocidos por internet este juego sería 100% suerte, sin embargo, tienes varias rondas para conocer a tus oponentes, y la premisa principal es que todos van a querer ganar. Con esos datos en mente puedes desarollar estrategias y cálculos como los del Rey de Diamantes.
La mejor estrategia parece ser sin duda medir la racionalidad de tus oponentes y actuar en consecuencia. No es una gran ayuda, pero tampoco sé qué otras estrategias se podrían emplear. Si tienes alguna idea, déjala en los comentarios.
FIN – El Juego del Rey de Diamantes de Alice in Borderland
Este ha sido un resumen y análisis del juego Concurso de Belleza, puesto en práctica en un escenario teórico de Alice in Borderlands, tras su propuesta matemática por Keynes en 1936, y su transformación a formato «juego» por Colin F. Camerer unos años después.
Puedes dejar un comentario con tu opinión, o resaltando cualquier dato que creas que es incorrecto o puede ser mejorado; estaré encantado de leerlo.
