Muy buenas. Hoy estaba en mi empresa trabajando cuando he escuchado brevemente hablar sobre la ordenación de grandes Bases de Datos y el tiempo que puede acarrear esta tarea, y me he preguntado «¿cuáles son los mejores algoritmos para ordenar grandes cantidades de datos?«. Es por eso que hoy traigo un artículo sobre algunos de los algoritmos de ordenación más populares, con su uso, rendimiento, y consumo de memoria.
Mejores Algoritmos de Ordenación de Datos
Ordenamiento de Burbuja
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Burbuja | Intercambio | n^2 | n^2 | n^2 | 1 |
Este algoritmo de ordenación funciona de la siguiente forma: Recorre una lista comparando simpre un elemento y el siguiente. Si no están en el orden deseado, se les da la vuelta y continúa con los siguientes elementos de la lista. Este proceso se repite tantas veces como elementos tenga la lista.
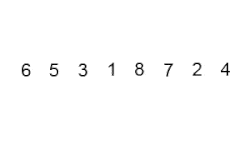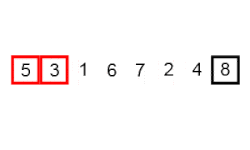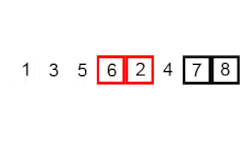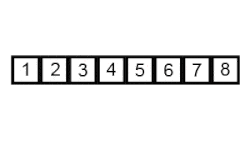
El algoritmo de Ordenamiento de Burbuja es uno de los más sencillos que existen, con una implementación bastante intuitiva y un rendimiento de n^2. Esto significa que puede tener un rendimiento decente para pequeños grupos de elementos, pero no va a ser eficaz en el caso de tener un gran grupo de elementos para ordenar, porque el tiempo que tardará en ordenar el conjunto aumentará de forma exponencial. Un dato curioso sobre este algoritmo de ordenación es que es el más lento de todos en ordenar una lista de elementos que ya está ordenada. Por este motivo se considera uno de los algoritmos más ineficientes de todos, y únicamente se usa en clases de programación para introducir estos algoritmos, debido a su simplicidad.
Ordenamiento Rápido
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Rápido | Partición | n * log(n) | n * log(n) | n^2 | log n |
Este algoritmo de ordenación funciona de la siguiente forma: Se selecciona aleatoriamente un elemento de la lista y se utiliza como divisor. Se ordenarán después todos los elementos tanto a su derecha como a su izquierda, y de esta manera se crean dos nuevas sublistas. En cada una de estas sublistas volvemos a repetir el proceso hasta que se creen sublistas con un único elementos. Cuando todas las sublistas tengan solo un elemento, se detiene la ejecución.
Aunque en el GIF mostrado arriba parezca un proceso complicado y lento, en realidad es el mejor algoritmo para ordenar conjuntos gigantes de datos, ya que gracias a su implmentación el tiempo que tarda el ordenar una lista aumenta de forma logarítmica, y no de forma constante o exponencia como ocurre en otros casos. Además en la mayoría de casos se suele aplicar antes un algoritmo de selección para decidir de manera bastante acertada cuál será el pivote o divisor inicial, ayudándose a situarse más cerca de su rendimiento óptimo que de su rendimiento en el peor caso. Otro punto muy a favor del Ordenamiento Rápido frente a otros algoritmos de rendimiento n * log(n) es que este es el que menos intercambios innecesarios de elementos realiza. Eso lo convierte en el algoritmo óptimo para ordenar listas gigantescas de datos.
Ordenamiento por Mezcla
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Mezcla | Mezcla | n * log(n) | n * log(n) | n * log(n) | n |
¿Cómo funciona este algoritmo?
Este algoritmo de ordenación funciona de la siguiente forma: Primero divides toda lista de elementos en listas de un solo elemento. Esas listas las vuelves a juntar para crear listas de dos elementos, y las ordenas. Luego de esas listas comparas siempre el primer elemento, y los mueves en orden a una lista de cuatro elementos. Vuelves a repetir el proceso con listas de ocho elementos, y así hasta que de nuevo vuelvas a tener una única lista, que ya estará ordenada.
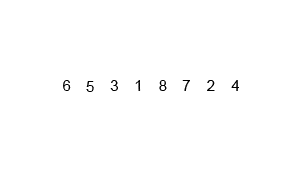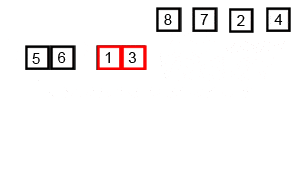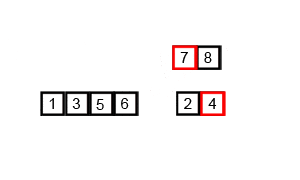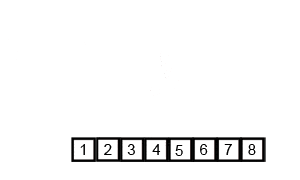
La ordenación por mezcla es también una de las más eficaces cuando se trata de grupos de elementos muy muy grandes, y puede ser superior al algoritmo de Ordenamiento Rápido si no elegimos bien el pivote de este último. Aún así, su consumo de memoria es mayor, y aplicar un segundo algoritmo para elegir bien el pivote en la Ordenación Rápida no cuesta tanto como el gasto de memoria que tiene este algoritmo.
Ordenamiento por Inserción
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Burbuja | Inserción | n | n^2 | n^2 | 1 |
¿Cómo funciona este algoritmo?
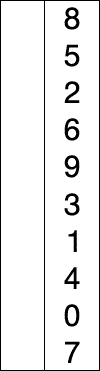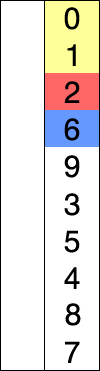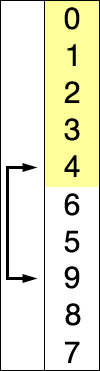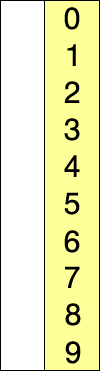
Este algoritmo de ordenación funciona de la siguiente forma: Comienza creando una lista nueva y saca el primer elemento de la lista inicial para añadirlo a la nueva. Luego extrae el segundo elemento de la lista inicial y lo inserta en la nueva de manera ordenada, siempre comparando de derecha a izquierda. Con el tercer y el resto de los elementos se comporta exactamente igual, hasta que la lista inicial queda vacía.
Este tipo de algoritmo de ordenación es especialmente útil para pequeños grupos de elementos, ya que aunque su rendimiento promedio es n^2 se beneficia enormemente de elementos que ya presentan cierto orden en la lista inicial. De este modo su rendimiento promedio puede verse modificado según el estado inicial de los elementos, y en grupos pequeños no es tán difícil que su rendimiento se acerque más a n * log(n) que a n^2.
Ordenamiento por Selección
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Selección | Selección | n^2 | n^2 | n^2 | 1 |
¿Cómo funciona este algoritmo?
Este algoritmo de ordenación funciona de la siguiente forma: Se recorre toda la lista de elementos y se va guardando siempre el más pequeño que se ha encontrado. Si mientras recorres la lista encuentras uno más pequeño que el que habías encontrado antes, sustituyes el antiguo por el nuevo. Al llegar al final de la lista, ese elemento lo llevas a la primera posición, y empiezas de neuvo a recorrer la lista pero desde el segundo elemento. Así hasta que te toque empezar a recorrer la lista desde el último elemento.
Este algoritmo también presenta su mayor eficacia cuando tiene que ordenar grupos pequeños de elementos. Aún así, su única ventaja frente al algoritmo de inserción es que este se escribe con menos código y es más intuitivo para los seres humanos. De este modo, y al no ser capaz de ofrecer un rendimiento mejor que la ordenación por inserción, este algoritmo suele quedar relegado a un segundo lugar, y muy pocas veces se utiliza de manera profesional.
Ordenamiento por Montículos
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Montículos | Selección | n * log(n) | n * log(n) | n * log(n) | 1 |
Este algoritmo de ordenación funciona de la siguiente forma: Seleccionas el primer elemento de la lista y en él guardas dos espacios para el segundo y tercer elementos. Si alguno de estos elementos es más grande que el padre, los intercambias. Luego en cada uno de esos elementos hijos guardas otros dos números de la lista, y si alguno de esos números es más grande que el padre, los intercambias hasta que ningún elemento padre sea más pequeño que uno hijo. Repites este proceso hasta llegar al último elemento de la lista.
Luego vas desglosando este árbol de listas que has creado, y vas ordenando los elementos de arriba hacia abajo, sin tener que volver a revisar ninguno de los elementos que has ordenado una vez bajas al siguiente nivel del árbol.

Aunque es muy raro de implementar, matemáticamente hablando es el algoritmo más eficaz de todos. Sin embargo, aunque puede competir a la par con el Ordenamiento por Mezcla, suele quedarse por debajo del Ordenamiento Rápido, ya que este último no realiza apenas intercambios de datos innecesarios, y es un tiempo muy valioso que se ahorra.
Ordenamiento Radix
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Radix | No Comparativo | n * k | n * k | n * k | n |
Este algoritmo de ordenación funciona de la siguiente forma: Cualquier valor de la lista se transforma en número, y de cada número en la lista, comparas el dígito de la derecha, y creas grupos según su valor. Luego, de esos grupos comparas el segundo dígito de la derecha (si no existe, lo creas como un 0), y vuelves a crear grupos y a ordenarlos según su valor y el grupo al que pertenecían. Este proceso se repite hasta que ningún número tiene más dígitos a la derecha.
Aunque matemáticamente hablando el rendimiento de este algoritmo puede ser mejor que el de cualquier otro en esta lista, la realidad es que la constante (k), que representa al número máximo de dígitos en un número de la lista, y con la que aumenta su rendimiento suele ser muchímo mayor que log(n), además de su consumo excesivo de memoria.
Ordenamiento por Casilleros
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Casilleros | No Comparativo | n | n + (n^2 / k) + k | n^2 | n |
Este algoritmo de ordenación funciona de la siguiente forma: Funciona similar al Ordenamiento Radix, ya que se comienza agrupando todos los elementos de la lista según diferentes grupos. Luego cada grupo se ordena con uno o varios algortimos extra, y de esta forma consigues que estos últimos algoritmos no se sobrecarguen tanto.
Ordenamiento por Cuentas
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Cuentas | No Comparativo | n + k | n + k | n + k | n + k |
Este algoritmo de ordenación funciona de la siguiente forma: Recorre la lista de elementos (solo admite números enteros) para seleccionar el mayor y el menor. Después crea grupos para cada número entre el más grande y el más pequeño, y al volver a recorrer la lista lo único que hace es mover cada elemento a su correspondiente grupo (existe un grupo por cada número).
No es un algoritmo eficiente si hay números con mucha diferencia de tamaño, pero suele usarse como sub-rutina en algoritmos como Radix o Ordenación por Cuentas debido a que estos dos algoritmos crean grupos más pequeños y de esta manera reducen mucho la diferencia de tamaño entre números.
Además también es un algoritmo relamente eficaz para ordenar grupos muy grandes de datos en los que el mayor dato es mucho más pequeño que el número total de elementos en la lista.
Otros Algoritmos Ineficaces
Ordenamiento Estúpido
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Estúpido | ? | n | n x n! | No termina | 1 |
Este algoritmo de ordenación funciona de la siguiente forma: Primero se comprueba si la lista de elementos está ordenada, y sino lo está se vuelve a reodenar toda la lista de elementos de manera aleatoria y se empieza de nuevo.
Ordenamiento de Tortitas / Panqueques
| Algoritmo | Método | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
| Tortitas / Panqueques | ? | n | n^2 | n^2 | 1 |
Este algoritmo de ordenación funciona de la siguiente forma: Recorres la lista de elementos para ver cuál es el mayor, y desde el primer elemento hasta ese, inviertes el orden de todos los elementos, para que el mayor quede arriba del todo. Después inviertes el orden de todos los elementos de la lista, para que el mayor quede abajo. Luego repites este proceso hasta que no queden elementos para voltear.
Resumen de los mejores algoritmos según su rendimiento
Aunque no existe un algoritmo definitivo para ordenar una lista de elementos, sí que es verdad que no todos tienen el mismo rendimiento dependiendo de los casos a los que se enfrenten. De este modo existen algoritmos que brillan para casos concretos, y otros que lo hacen de manera general, como el Ordenamiento Rápido a la hora de ordenar grupos gigantescos de datos, o el Ordenamiento por Inserción cuando se trata de ordenar grupos de datos de un tamaño relativamente pequeño.
| Nombre del Algoritmo | Mejor Rendimiento | Rendimiento Promedio | Peor Rendimiento | Memoria |
|---|---|---|---|---|
| Ordenamiento Rápido | Ω (n * log(n)) | Θ (n * log(n)) | O (n^2) | O (log n) |
| Ordenamiento Burbuja | Ω (n) | Θ (n^2) | O (n^2) | O (1) |
| Ordenamiento por Mezcla | Ω (n * log(n)) | Θ (n * log(n)) | O (n * log(n)) | O (n) |
| Ordenamiento por Inserción | Ω (n) | Θ (n^2) | O (n^2) | O (1) |
| Ordenamiento por Selección | Ω (n^2) | Θ (n^2) | O (n^2) | O (1) |
| Ordenamiento por Montículos | Ω (n * log(n)) | Θ (n * log(n)) | O (n * log(n)) | O (1) |
| Ordenamiento Radix | Ω (n * k) | Θ (n * k) | O (n * k) | O (n) |
| Ordenamiento por Casilleros | Ω (n + k) | Θ (n+k) | O (n^2) | O (n) |
| Ordenamiento por Cuentas | Ω (n + k) | Θ (n + k) | O (n + k) | O (n + k) |
| Ordenamiento Estúpido | Ω (n) | Θ (n x n!) | O (∞) Infinito | O (1) |
| Ordenamiento Panqueque / Tortita | Ω (n) | Θ (n^2) | O (n^2) | O (1) |
